A geometria forgási alakjai különös figyelmet kapnak jellemzőik és tulajdonságaik tanulmányozása során. Az egyik egy csonka kúp. Ennek a cikknek a célja annak a kérdésnek a megválaszolása, hogy a csonka kúp területe milyen képlettel számítható ki.
Milyen számról fogunk beszélni?
A csonka kúp területének leírása előtt meg kell adni ennek az ábrának a pontos geometriai meghatározását. A csonka kúp olyan kúp, amelyet egy közönséges kúp csúcsának síkkal történő levágása eredményeként kapunk. Ebben a meghatározásban számos árnyalatot kell hangsúlyozni. Először is, a szakasz síkjának párhuzamosnak kell lennie a kúp alapjának síkjával. Másodszor, az eredeti alaknak kör alakú kúpnak kell lennie. Természetesen lehet elliptikus, hiperbolikus vagy más típusú számok, de ebben a cikkben csak egy kör alakú kúpra korlátozódunk. Ez utóbbit az alábbi ábra mutatja.
Könnyű kitalálni, hogy nemcsak síkszakasz használatával, hanem a forgási művelet használatával is megszerezhető. Ehhez vegyen egy két derékszögű trapéz alakot, majd forgassa el az ezen derékszögekkel szomszédos oldal körül. Ennek eredményeként a trapéz alapjai a csonka kúp alapjainak sugarai lesznek, a trapéz oldalirányú ferde oldala pedig a kúpos felületet írja le.
Az alak kibontása
Figyelembe véve a csonka kúp felületét, hasznos a sweep, vagyis a háromdimenziós alak felületének képe a síkban. Az alábbiakban a vizsgált ábra tetszőleges paraméterekkel történő beolvasása látható.
Látható, hogy az ábra területét három komponens alkotja: két kör és egy csonka kör alakú szegmens. Nyilvánvaló, hogy a kívánt terület meghatározásához össze kell adni az összes megnevezett szám területét. Oldjuk meg ezt a problémát a következő bekezdésben.
A csonka kúp területe
A következő érvek megértésének megkönnyítése érdekében a következő jelölést vezetjük be:
- r1, r2 a nagy, illetve a kis bázisok sugara;
- h az ábra magassága;
- g-alakú kúp (a trapéz ferde oldalának hossza).
A csonka kúp alapjainak területe könnyen kiszámítható. Írjuk le a megfelelő kifejezéseket:
So1 = P * r12;
So2 = P * r22.
A kör alakú szegmens egy részének területét valamivel nehezebb meghatározni. Ha elképzeljük, hogy ennek a kör alakú szektornak a középpontja nincs kivágva, akkor sugara megegyezik a G értékével. Nem nehéz kiszámítani, ha figyelembe vesszük a megfelelő hasonlót derékszögű háromszögek a kúp. Ez egyenlő:
G = r1* g / (r1-r2).
Ezután az egész kör alakú szektor területe, amely a G sugárra épül, és amely 2*pi*r hosszúságú íven nyugszik1, egyenlő lesz:
S1 = P * r1* G = pi * r12* g / (r1-r2).
Most határozza meg egy kis kör alakú szektor területét S2, amit ki kell vonni az S-ből1. Ez egyenlő:
S2 = P * r2* (G - g) = pi * r2* (r1* g / (r1-r2)- g) = pi * r22* g / (r1-r2).
A kúpos csonka felület területe Sb egyenlő a különbséggel S1 és S2. Kapunk:
Sb = S1 - S2 = P * r12* g / (r1-r2)- pi * r22* g / (r1-r2) = pi * g*(r1+r2).
A kissé nehézkes számítások ellenére meglehetősen egyszerű kifejezést kaptunk az ábra oldalfelületének területére.
A bázisok és S területek összeadásab, , a csonka kúp területének képletéhez jutunk:
S = So1 + So2 + Sb = P * r12 + pi * r22 + P * g*(r1+r2).
Így a vizsgált ábra s nagyságának kiszámításához meg kell ismerni annak három lineáris paraméterét.
Példa egy feladatra
Egy 10 cm sugarú, 15 cm magasságú kör alakú egyenes kúpot egy sík levágott úgy, hogy szabályos csonka kúpot kapjunk. Tudva, hogy a csonka alak alapjai közötti távolság 10 cm, Meg kell találni a felületének területét.
A csonka kúp terület képletének használatához meg kell találni három paraméterét. Egy tudjuk:
r1 = 10 cm.
A másik kettő könnyen kiszámítható, ha hasonló téglalap alakú háromszögeket veszünk figyelembe, amelyeket a kúp tengelyirányú szakaszának eredményeként kapunk. Figyelembe véve a problémás állapotot, megkapjuk:
r2 = 10 * 5/15 = 3,33 cm.
Végül a csonka g kúp vezetője egyenlő lesz:
g = √(102 + (r1-r2)2) = 12,02 cm.
Most helyettesítheti az R értékeket1, r2 és g az S képletébe:
S = pi * r12 + pi * r22 + P * g*(r1+r2) = 851,93 cm2.
Az ábra kívánt felülete körülbelül 852 cm2.
Az egyenes prizma felülete: képletek és egy probléma példája
Prizma térfogat képlete. Szabályos négyszög és hatszög alakú térfogat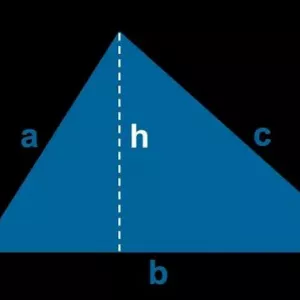
Heron képlete, vagy hogyan lehet megtalálni a háromszög területét három oldalon
A ház nappali területe: mit tartalmaz, számítási szabályok
Olaj a dízelmotor közbenső hűtőjében: a probléma megoldásának okai és módszerei
Nátrium-guanilát: az élelmiszer-adalékanyag képlete, az emberi testre gyakorolt hatás
Miért öntözik az egyik szem egy felnőttnél: okok, a probléma megoldásának módszerei és az orvosok tanácsai
Az emberi test területe: számítási képlet és számítási példák
A szülői felügyelet elhelyezése a youtube-on? A probléma megoldásának különböző módjai