Tartalom
A sztereometria a háromdimenziós geometriai alakzatok jellemzőit vizsgálja. A geometriai problémákban megjelenő egyik jól ismert háromdimenziós ábra egy egyenes prizma. Nézzük meg ebben a cikkben, hogy mi az, valamint részletesen írja le a háromszög alakú prizmát.
Prizma és típusai
A prizma olyan alakot jelent, amely a sokszög térben történő párhuzamos átvitelének eredményeként alakul ki. Ennek a geometriai műveletnek az eredményeként egy ábra alakul ki, amely több paralelogrammából és két azonos sokszögből áll egymással párhuzamosan. A paralelogrammok a prizma oldalai, a sokszögek pedig az alapjai.
Bármely prizmának n+2 oldala, 3 * n éle és 2 * n csúcsa van, ahol n a sokszögű alap sarkainak vagy oldalainak száma. A képen egy ötszögletű prizma látható, amely 7 oldalból, 10 csúcsból és 15 élből áll.

A vizsgált számok osztályát többféle prizma képviseli. Soroljuk fel őket röviden:
- konkáv és konvex;
- ferde és egyenes;
- rossz és helyes.
Minden szám a felsorolt három osztályozási típus egyikéhez tartozik. A geometriai problémák megoldásakor a legegyszerűbb elvégezni számítások helyes és egyenes prizmák. Az utóbbit részletesebben megvizsgáljuk a cikk következő bekezdéseiben.
Mi ez-egyenes prizma?
Az egyenes vonalat konkávnak vagy konvexnek nevezzük, rendszeres vagy szabálytalan prizma, amelyben az összes oldalt négyszögek képviselik, szöge 90^. Ha az oldalak legalább egy négyszöge nem téglalap vagy négyzet, akkor a prizmát ferdenek nevezzük. Megadhat egy másik meghatározást is: az egyenes prizma ennek az osztálynak az alakja, amelyben bármely oldalsó él megegyezik a magassággal. A prizma h magassága alatt feltételezzük a bázisok közötti távolságot.
A közvetlen prizma mindkét fenti meghatározása egyenlő és önellátó. Ebből következik, hogy a bázisok és mindkét oldal közötti összes dihedrális szög egyenlő 90 xhamsterrel.
A fentiekben azt mondták, hogy a problémák megoldása során kényelmes egyenes számokkal dolgozni. Ez annak köszönhető, hogy a magasság egybeesik az oldalsó él hosszával. Ez utóbbi tény megkönnyíti az ábra térfogatának és az oldalfelület területének kiszámítását.

Az egyenes prizma térfogata
A térfogat bármely térbeli alakra jellemző mennyiség, amely numerikusan tükrözi a vizsgált tárgy felületei között bezárt tér egy részét. A prizma térfogata a következő általános képlettel számítható ki:
V = So* h.
Vagyis a magasság szorzata az alap területével megadja a kívánt értéket V. Mivel az egyenes prizma alapjai egyenlőek, akkorezek közül bármelyik lehet használni, hogy meghatározza a terület S o.
A fenti képlet kifejezetten egyenes prizmához való alkalmazásának előnye a többi típushoz képest az, hogy nagyon könnyű megtalálni az ábra magasságát, mivel egybeesik az oldalsó él hosszával.
Oldalfelület
Kényelmes kiszámítani nemcsak a szóban forgó osztály egyenes alakjának térfogatát, hanem annak oldalfelületét is. Valójában bármelyik oldala téglalap vagy négyzet. Minden hallgató tudja, hogyan kell kiszámítani ezeknek a lapos alakoknak a területét, ezért a szomszédos oldalakat meg kell szorozni egymással.
Tegyük fel, hogy a prizma alján egy tetszőleges n-gon található, amelynek oldalai egyenlőek ai. Az I index az 1-től n-ig terjedő értékeken halad át. Egy téglalap területét a következőképpen kell kiszámítani:
Si = ai* h.
Az S oldal felületeb nem nehéz kiszámítani, ha összeadjuk az összes területen Si téglalapok. Ebben az esetben megkapjuk az S végső képletétb egyenes prizma:
Sb = h*∑i=1n(ai) = h * Po.
Így az egyenes prizma oldalfelületének meghatározásához meg kell szorozni annak magasságát egy alap kerületével.
A háromszög alakú prizma problémája

Tegyük fel, hogy egyenes prizma van megadva. Alapozás - derékszögű háromszög. A háromszög lábai 12 cm és 8 cm. Az ábra térfogatát és teljes területét ki kell számítani, ha a prizma magassága 15 cm.
Először számítsuk ki az egyenes prizma térfogatát. Az alapjain elhelyezkedő háromszög (téglalap alakú) területe:
So = a1* a2/2 = 12 * 8/2 = 48 cm2.
Mint sejteni lehet, a1 és a2 ebben az egyenlőségben katéták vannak. Ismerve a terület a bázis és a magasság (lásd. a probléma állapota), használhatja a v képletet:
V = So* h = 48 * 15 = 720 cm3.
Az ábra teljes területét két rész alkotja: az alapok és az oldalfelület területei. A két bázis területe egyenlő:
S2o = 2 * So = 48 * 2 = 96 cm2.
Az oldalsó felület területének kiszámításához meg kell ismerni a derékszögű háromszög kerületét. A Pitagorasz-tétel alapján kiszámítjuk az a hipotenuszát3, van:
a3 = √(a12 + a22) = √(122 + 82) = 14,42 lásd.
Ezután az egyenes prizma alapjának háromszögének kerülete lesz:
P = a1 + a2 + a3 = 12 + 8 + 14,42 = 34,42 cm.
Az S képlet alkalmazásab, ez volt írva az előző bekezdésben, megkapjuk:
Sb = h * P = 15*34,42 = 516,3 cm.
A terület összeadása S2o és Sb, megkapjuk a vizsgált geometriai alak teljes felületét:
S = S2o + Sb = 96 + 516,3 = 612,3 cm2.

A speciális típusú üvegből készült háromszög alakú prizmát az optikában használják a fénykibocsátó tárgyak spektrumának tanulmányozása során. Az ilyen prizmák a diszperzió jelensége miatt képesek a fényt komponens frekvenciákra bontani.
 Az egyenes prizma felülete: képletek és egy probléma példája
Az egyenes prizma felülete: képletek és egy probléma példája Geometriai alakú prizma. A térfogat és a terület tulajdonságai, típusai, képletei. Szabályos háromszög alakú prizma
Geometriai alakú prizma. A térfogat és a terület tulajdonságai, típusai, képletei. Szabályos háromszög alakú prizma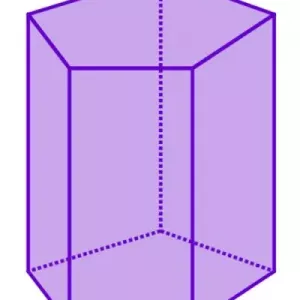 Prizma térfogat képlete. Szabályos négyszög és hatszög alakú térfogat
Prizma térfogat képlete. Szabályos négyszög és hatszög alakú térfogat Mi ez-normál gyorsulás? Az előfordulás oka és a képlet. Példa egy feladatra
Mi ez-normál gyorsulás? Az előfordulás oka és a képlet. Példa egy feladatra Hogyan mérik a mechanikai munkát? A gáz működésének képletei és az erő pillanata. Példa egy feladatra
Hogyan mérik a mechanikai munkát? A gáz működésének képletei és az erő pillanata. Példa egy feladatra Mi az a tangenciális gyorsulás?? Képletek, példa egy problémára
Mi az a tangenciális gyorsulás?? Képletek, példa egy problémára Az ideális gázmolekulák koncentrációja. Képletek és példa egy problémára
Az ideális gázmolekulák koncentrációja. Képletek és példa egy problémára Ideális gáz. A clapeyron-mendelejev egyenlet. Képletek és példa egy problémára
Ideális gáz. A clapeyron-mendelejev egyenlet. Képletek és példa egy problémára Fekete ametiszt: fotó és leírás a kő, tulajdonságok, aki alkalmas az állatöv jel
Fekete ametiszt: fotó és leírás a kő, tulajdonságok, aki alkalmas az állatöv jel