A planimetria a geometria fontos ága, amely a sík alakzatokat vizsgálja. Az összes ilyen elem fő tulajdonsága az általuk elfoglalt terület. Vizsgáljuk meg a cikkben, hogy milyen képleteket használnak a kör területének kiszámításához.
Mi ez?
Nyilvánvaló, hogy a kör területének kiszámítása előtt meg kell adni az ábra geometriai meghatározását. Ez alatt a sík azon pontjainak halmazát értjük, amelyek egy adott o ponttól az R értékével kisebb vagy egyenlő távolságban helyezkednek el. Az O pontot a kör középpontjának nevezzük, R pedig a sugara.

A körrel ellentétben a körnek van egy bizonyos területe. A kör határolja a kört. Hossza a vizsgált ábra kerülete.
A sugár és a középpont mellett a kört d átmérő is jellemzi. Minden olyan szegmenst képvisel, amely áthalad az ábra közepén.
Egy kör akkor érhető el, ha egy bizonyos szegmenst veszünk, rögzítjük az egyik végét a síkon, és forgassuk el a szabad véget a rögzített pont körül 360-mal o. Ebben az esetben a szegmens hossza az ábra sugara lesz.
Képletek a kör területének kiszámításához

Az ábra területét a sík területének nevezzük, amelyet egy kör határol. Azonnal megtudjuk, hogy a kérdéses ábra területét nem lehet pontosan meghatározni, azonban ez a pontosság a tizedespont után bármely jelentős számjegyre növelhető. A helyzet az, hogy a területképlet tartalmazza a Pi (pi)számot. Hozzávetőleges jelentése már az ókori Egyiptomban ismert volt. A tizedesjegy után néhány számjegy pontossággal azonban Leonhard Euler határozta meg 1737-ben. Azt is javasolta, hogy hívja "a Pi szám". Legfeljebb öt számjegyű pontosság 3.14159.
A kör területének kiszámítása a következő képletekkel történik:
S = pi * r2;
S = pi * d2 / 4;
S = L * r / 2.
Az első két egyenlet érthető, mert a sugár és az átmérő közötti kapcsolat kifejezését használják. Ami a harmadik képletet illeti, akkor kapjuk meg, ha az L kör kerületére használjuk a kifejezést. Emlékezzünk arra, hogy L = 2 * pi * r.
A fenti képen látható egy példa a probléma megoldására. A területet ebben az esetben az a betű jelzi.
 Kötvényhozam: számítási képlet
Kötvényhozam: számítási képlet Alkohol denat-mi ez: képlet, előállítási módszer, alkalmazás, hatás a testre
Alkohol denat-mi ez: képlet, előállítási módszer, alkalmazás, hatás a testre Mi ez-normál gyorsulás? Az előfordulás oka és a képlet. Példa egy feladatra
Mi ez-normál gyorsulás? Az előfordulás oka és a képlet. Példa egy feladatra Foszfatidilkolin: képlet, összetétel, tulajdonságok és alkalmazás
Foszfatidilkolin: képlet, összetétel, tulajdonságok és alkalmazás A windows 10 újratelepítése adatvesztés nélkül: három egyszerű módszer
A windows 10 újratelepítése adatvesztés nélkül: három egyszerű módszer A hangszóró q-tényezője: számítási képlet, hogyan lehet csökkenteni vagy növelni a hangszóró q-tényezőjét
A hangszóró q-tényezője: számítási képlet, hogyan lehet csökkenteni vagy növelni a hangszóró q-tényezőjét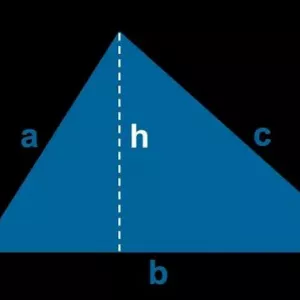 Heron képlete, vagy hogyan lehet megtalálni a háromszög területét három oldalon
Heron képlete, vagy hogyan lehet megtalálni a háromszög területét három oldalon Tabakov filmjei: a tavasz tizenhét pillanata,d 'artagnan és a három testőr, a capuchin boulevard embereés mások
Tabakov filmjei: a tavasz tizenhét pillanata,d 'artagnan és a három testőr, a capuchin boulevard embereés mások Kalória blokkoló három fázis: a fogyás áttekintése
Kalória blokkoló három fázis: a fogyás áttekintése